Кенигсберг был построен на берегу реки Прегель (Преголя), которая разделила город на четыре отдельных жилых массива. Люди перебирались из одного района в другой через семь различных мостов. Согласно легенде, популярным развлечением во время воскресных прогулок были попытки пройти через весь город так, чтобы пересечь каждый мост только один раз. Никто так и не придумал, как это сделать, но это вовсе не значит, что задача не имеет решения.
Им просто нужно было обратиться к подходящему эксперту, чтобы узнать его.
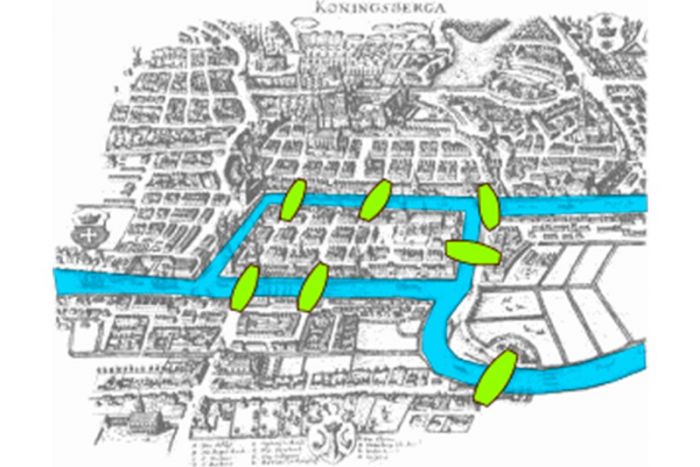В 1735 году мэр города Данцига (ныне польский Гданьск), расположенного в 120 километрах к западу от Кенигсберга, Карл Леонард Готлиб Эйлер, обратился к Леонарду Эйлеру с письмом, в котором просил о помощи в решении этой задачи от имени местного профессора математики по имени Генрих Кюн. Уже тогда Эйлер был знаменитым и весьма успешным математиком – он опубликовал свою первую книгу в течение года после этого письма, а за всю жизнь написал более 500 книг и статей.
Поэтому неудивительно, что сначала Эйлер подумал, что заниматься решением этой задачи ниже его достоинства, и написал в ответ: «Итак, вы видите, досточтимый сэр этот тип решения практически не имеет отношения к математике, и я не понимаю, почему вы обращаетесь с такой просьбой к математику, а не к кому-то еще, поскольку решение основано только на здравом смысле и не зависит ни от одного из известных математических принципов».
Однако, в конце концов, Элеру и Кюну удалось убедить Эйлера, и он понял, что это был совершенно новый тип математики – «геометрия положений», сегодня известная как топология. В топологии точная форма или расположение объекта не имеют значения. Есть даже старая шутка о том, что тополог не в состоянии определить разницу между пончиком и кофейной чашкой, поскольку оба предмета имеют ровно одно отверстие. Об этой совершенно новой области математики до тех пор только писали, но никто еще не понимал, какие проблемы она способна решать. Семь мостов Кенигсберга были прекрасным экспериментальным подтверждением новой теории, поскольку задача не требовала каких-либо измерений или точных расчетов. Можно превратить сложную карту города в простой и понятный граф (схему), не теряя при этом никакой важной информации.
Хотя у кого-то может возникнуть соблазн решить эту задачу, наметив все возможные маршруты через город, Эйлер сразу осознал, что эта стратегия потребует слишком много времени и не будет работать с другими схожими задачами (что, если в другом городе будет, скажем, двенадцать мостов?). Вместо этого он решил на время отвлечься от мостов и пометил участки суши буквами A, B, C и D. Таким образом, он теперь мог описать путешествие через мост из района А в район В как АВ, а путешествие из района А через район В район D как АВD. Здесь важно отметить, что количество букв в описании маршрута всегда будет на единицу больше, чем количество пересекаемых мостов. Так, маршрут АВ пересекает один мост, а маршрут АВD – два моста, и так далее. Эйлер понял, что поскольку в Кенигсберге семь мостов, а для того, чтобы пересечь их все, маршрут должен состоять из восьми букв, значит, решение задачи потребует именно восьми букв.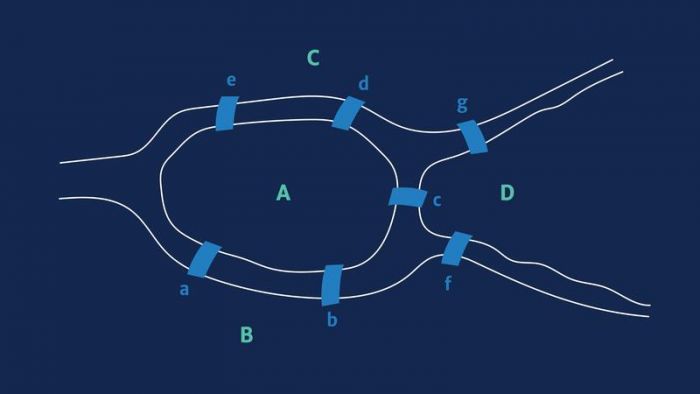
Затем он придумал более общее правило, используя еще более упрощенную схему. Если бы у вас было всего два сухопутных участка, А и В, и вы пересекали мост один раз, то участок А мог бы быть там, где путешествие начиналось, или там, где оно заканчивалось, но вы находились бы на участке А только однажды. Если бы вы пересекали мосты а, b и c по одному разу, то оказались бы на участке А ровно два раза. Это привело к созданию удобного правила: если у вас имеется четное число мостов, ведущих на один участок суши, вы должны добавить к этому числу единицу, а затем разделить полученную сумму на два, чтобы выяснить, сколько раз этот участок должен использоваться в ходе путешествия. (в данном примере, добавив единицу к количеству мостов, то есть к 3, получаем четыре, а разделив четыре на два получаем два, то есть именно дважды в путешествии пересекается участок А).
Этот результат вернул Эйлера к первоначальной проблеме. Есть пять мостов, которые ведут к участку А, поэтому в восьмибуквенном решении, которое он ищет, его придется пересекать три раза. У участков В, С и D есть по два моста, которые ведут к ним, поэтому каждый из них должен пересекаться дважды. Но 3+2+2+2 – это 9, а не 8, хотя по условию нужно пройти только через 8 участков и пересечь 7 мостов. Это означает, что невозможно пройти через весь город Кенигсберг, использовав каждый мост ровно один раз. Другими словами, в данном случае задача не имеет решения.
Однако, как и всякий истинный математик, Эйлер на этом не остановился. Он продолжал работать и создал более общее правило для других городов с другим количеством мостов. Если в городе нечетное количество мостов, то существует простой способ выяснить, можете ли вы совершить такое путешествие или нет: если сумма количества появлений каждой буквы, обозначающей участок земли, на единицу больше, чем количество мостов (как, например, в восьмибуквенном решении, о котором упоминалось ранее), такое путешествие возможно. Если же сумма больше этого числа, оно невозможно.
А как насчет четного количества мостов? В этом случае все зависит от того, с чего начать. Если вы начинаете с участка А и путешествуете по двум мостам, А в вашем решении появится дважды. Если вы начнете с другой стороны, то А появится только один раз. Если имеется четыре моста, тогда А появляется три раза, если этот участок был отправной точкой, или два раза, если не был. В общем виде это означает, что, если путешествие не начинается с участка А, он должен пересекаться вдвое меньшее количество раз, чем число мостов (четыре деленное на два дает два). Если же путешествие начинается с участка А, тогда он должен пересекаться на один раз больше.
Гениальность решения Эйлера заключается даже не в ответе, а в методе, который он применил. Это был один из первых случаев использования теории графов, также известной как теория сетей, весьма востребованной области математики в современном мире, заполненном транспортными, социальными и электронными сетями. Что касается Кенигсберга, в городе в конечном итоге появился еще один мост, который сделал решение Эйлера спорным, а затем британские войска разрушили большую часть города во время второй мировой войны. Сегодня и город и река имеют новые названия, но старинная задача живет в совершенно новой области математики.
